Neural Network Building Blocks

Deep learning is hot. New architectures are published all the time, setting the state of the art on a huge variety of different tasks.

Research is outpacing application. Exotic new architectures are being created so frequently that it’s difficult to keep track of what’s out there. The practitioner is drowning in options.

It helps to take a modular perspective. Each new paper features a new architecture, but usually it’s just a new arrangement of familliar building blocks, maybe with one or two totally novel components.

This page is intended as a reference guide to the building blocks of neural networks. It covers how they work, what they accomplish, and how to use them.

Layers and units

Neural networks are made up of layers. Sometimes we construct a single logical layer out of multiple simple layers. These compound layers are sometimes called units, as in “Gated Recurrent Unit”.

A layer takes a vector as input and produces another vector, not necessarily of the same size, as output.

Vanilla

A linear transformation of the input followed by a nonlinearity.

Mathematical defintion

A vanilla layer $h$ can be defined for a weight matrix $W$ , bias vector $b$ , and a nonlinearity $f$ :

$h(x) = f(Wx + b)$

Useful for: mapping from one feature space to another

Softmax

Turns an input vector into a categorical probability distribution.

Softmax layers take an input vector and return another vector of the same dimensionality whose elements are each between 0 and 1 and also sum to 1. This makes the output vector suitable to be interpreted as a categorical probability distribution.

Mathematical defintion

For an $n$ -dimensional input vector $x$ , each element $i$ of a softmax layer’s output is defined as:

$softmax(x)_i = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}$

Useful for: multiclass classification, attention

Embedding

A lookup table from some symbol to a vector that represents it in a high dimensional space.

Embedding layers often find use in natural language processing tasks, where they can be used to map from a word to a vector that represents the semantics of that word which can then be used as normal with other layers.

Embedding layers are often represented as matrices where each row is the vector for a particular symbol. These matrices can be multiplied by a one-hot vector for the target symbol to retrieve the embedded vector.

Useful for: converting discrete symbols into dense vector representations

Max pooling

Downsamples the input, selecting the maximum value in each region.

Max pooling layers segment the input into regions and return the max value from each. Typically, the result of a pooling operation is a tensor with the same number of axes as the input, but with fewer indices along each axis i.e. the input tensor is shrunk, but not flattened.

Useful for: dimensionality reduction, especially in image or speech processing

Gated Recurrent Unit (GRU)

A recurrent unit that uses gates to manage long-term dependencies.

A GRU

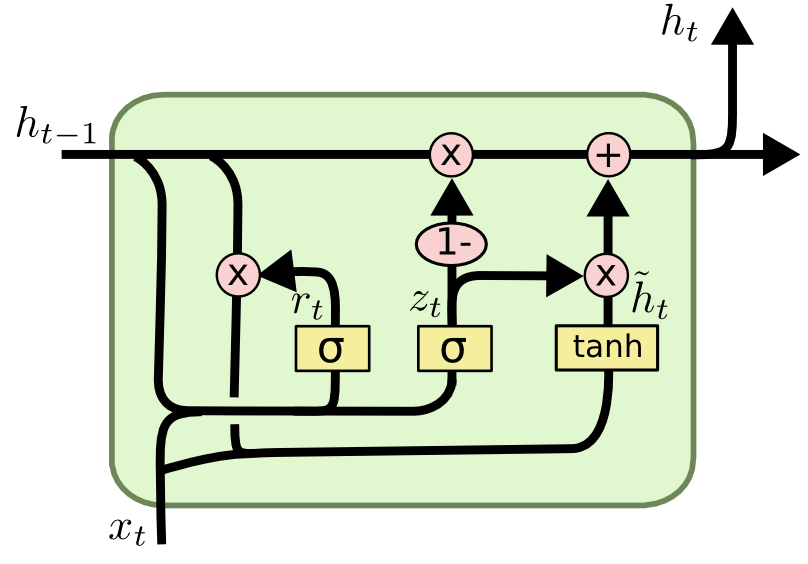
The internals of a GRU*

The output vector, or hidden state, of a GRU at a given time step depends on the current element of the sequence as well as the hidden state generated by the GRU at the previous time step. The flow of information from the input at a time step to the output is controlled by two internal layers called the update gate and the reset gate.

Mathematical defintion

At each time step, we compute the values of the two gates, the update gate $z_t$ , and the reset gate $r_t$ . They are parameterized by $W^{(z)}$ and $W^{(r)}$ , weight matrices for incorporating the current element of the input sequence, $x_t$ , and $U^{(z)}$ and $U^{(r)}$ , weight matrices for incorporating the previous hidden state, $h_t$ . We use the sigmoid activation function $\sigma$ to ensure that the elements of these gate vectors are between zero and one:

$z_t = \sigma(W^{(z)}x_t + U^{(z)}h_{t-1}) \\ r_t = \sigma(W^{(r)}x_t + U^{(r)}h_{t-1})$

We then compute $\widetilde{h}_t$ , often called the proposed hidden state update. $\circ$ is the Hadamard or elementwise product. The reset gate vector $r_t$ can be seen as controlling how much each element of the previous hidden state is allowed to enter into the proposed hidden state update $\widetilde{h}_t$ . If an element of $r_t$ is close to zero, $h_{t-1}$ has little influence on the next hidden state; the state is reset.

$\widetilde{h}_t = \tanh(Wx_t + r_t \circ Uh_{t-1})$

Finally, we combine the proposed hidden state update with the previous hidden state according to the update gate vector, $z_t$ . If an element of $z_t$ is close to 1, the corresponding element of the final hidden state $h_t$ will come almost entirely from $\widetilde{h}_t$ . If it’s close to zero, corresponding element of $h_{t-1}$ is carried through almost unchanged.

$h_t = z_t \circ h_{t-1} + (1 - z_t) \circ \widetilde{h}_t$

Useful for: processing sequences with long-distance dependencies

Long Short-Term Memory (LSTM)

A recurrent unit that uses gates and an internal memory cell to manage long-term dependencies.

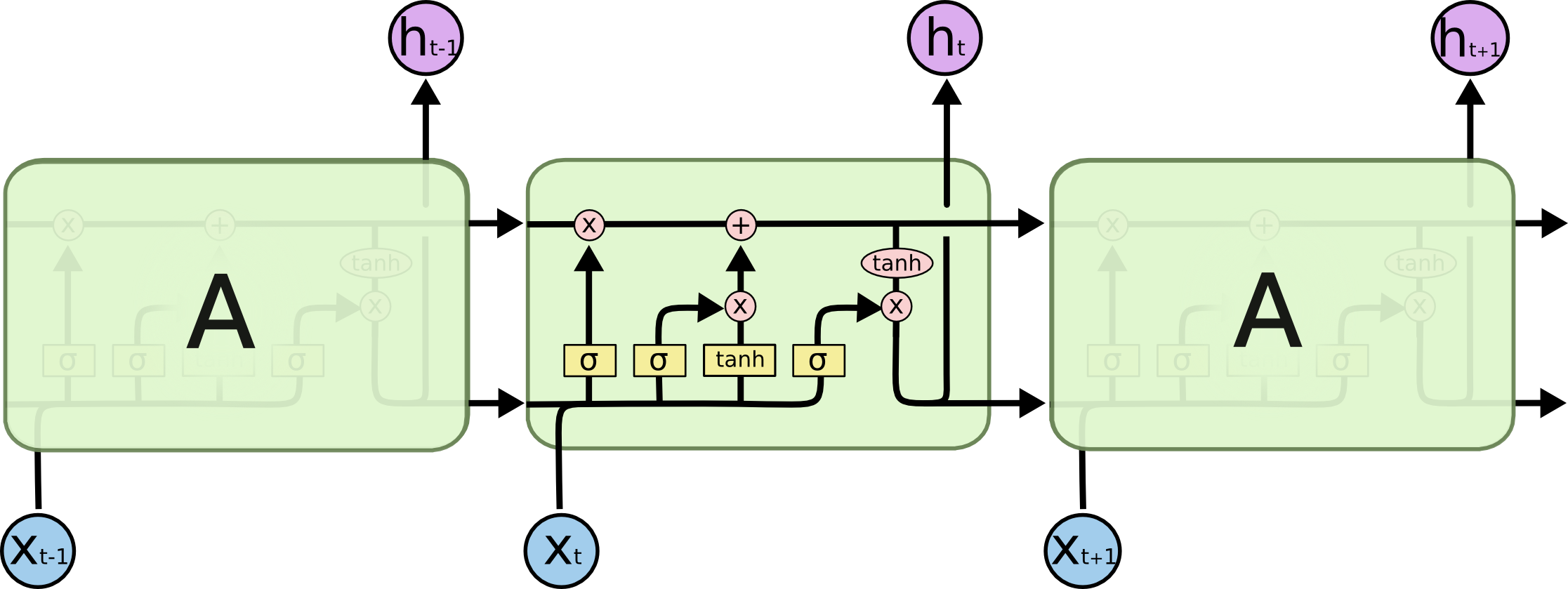
An LSTM

The internals of an LSTM*

LSTMs are a kind of layer used in recurrent neural networks. They maintain internal state in the form of a vector called the memory cell. At each time step, the network updates this memory cell based on its current input and allows information to flow out of the memory cell into the layer’s output. The flow of information into and out of the memory cell is controlled by internal layers called the input gate, the forget gate, and the output gate.

Mathematical defintion

At each time step, we compute the values of the three gates, the input gate $i_t$ , the forget gate $f_t$ , and the output gate $o_t$ for an input element $x_t$ and the previous hidden state $h_{t-1}$ . These gates are parameterized by $W^{(i)}$ , $W^{(f)}$ , and $W^{(o)}$ , weight matrices for incorporating the current element of the input sequence, and by $U^{(i)}$ , $U^{(f)}$ , and $U^{(o)}$ , weight matrices for incorporating the previous hidden state:

$i_t = \sigma(W^{(i)}x_t + U^{(i)}h_{t-1}) \\ f_t = \sigma(W^{(f)}x_t + U^{(f)}h_{t-1}) \\ o_t = \sigma(W^{(o)}x_t + U^{(o)}h_{t-1})$

To compute the new value of the memory cell $c_t$ , we first compute a proposed new memory cell $\widetilde{c}_t$ :

$\widetilde{c}_t = tanh(W^{(c)}x_t + U^{(c)}h_{t-1})$

The final memory cell is computed by combining the proposed new memory cell and the previous memory cell according to the forget and input gates. If $f_t$ is close to zero, the previous value of the memory cell is “forgotten”. If $i_t$ is close to zero, the new value of the memory cell is mostly unaffected by the current input element:

$c_t = f_t \circ c_{t-1} + i_t \circ \widetilde{c}_t$

Finally, we compute the new hidden state $h_t$ . The output gate $o_t$ controls the degree to which the value of the memory cell is output into the LSTM’s hidden state:

$h_t = o_t \circ tanh(c_t)$

Useful for: processing sequences with long-distance dependencies

Nonlinearities

Nonlinearities are critical to the expressive power of neural networks; they allow networks to represent nonlinear functions. A neural network layer typically applies some linear transformation to its input and then passes the transformed values through an element-wise nonlinearity to yield its final output, often called the layer’s activation.

Sigmoid

An s-shaped nonlinearity that produces activations between 0 and 1.

The sigmoid function and the hyperbolic tangent are related by a simple identity. The general guidance is to use the hyperbolic tangent instead of the signmoid except when one specifically needs activations between 0 and 1. See jpmuc’s answer at Cross Validated for more details.

Mathematical defintion

The sigmoid function, often denoted $\sigma$ , is defined for a scalar $x$ as:

$\sigma(x) = \frac{1}{1 + e^{-x}}$

Useful for: Producing activations between $0$ and $1$ , for example if the activations will be interpreted as probabilities.

Hyperbolic tangent (tanh)

An s-shaped nonlinearity that produces activations between $-1$ and $1$ .

Mathematical defintion

The hyperbolic tangent $tanh$ can be defined for a scalar $x$ as:

$tanh(x) = \frac{e^{2x} - 1}{e^{2x} + 1}$

Useful for: Producing activations between $-1$ and $1$ .

Rectifier

A nonlinearity that is simply the max of 0 and the input.

The rectifier is useful for avoiding the vanishing gradient problem. The gradient of a rectifier is either 0 or 1, so as error messages flow through it, they are either passed through unchanged, or zeroed out.

Mathematical defintion

The rectifier can be defined for a scalar $x$ as:

$f(x) = max(0, x)$

Useful for: deep networks, like recurrent networks over long sequences or deep convolution networks

Higher-order mechanisms

Just about every neural network has more than a single layer. Neural network architectures typically combine individual layers according to recognizable patterns. These higher-order mechanisms give the network the power to operate over different kinds of inputs, perform more complex kinds of computation, or produce different kinds of outputs.

Stacked layers

Passing the output of one layer as the input to another.

Stacking is the simplest means of making a neural network deep and therefore more expressive. Some architectures contain dozens of stacked layers. Stacking allows a network to learn complex functions with fewer parameters than would be required by a shallow (but wider) network. This is because later layers in a stack can benefit from the processing that has already been done by earlier layers.

Useful for: Increasing a model’s expressive power

Convolution

The application of a single layer to sliding, overlapping windows of an input.

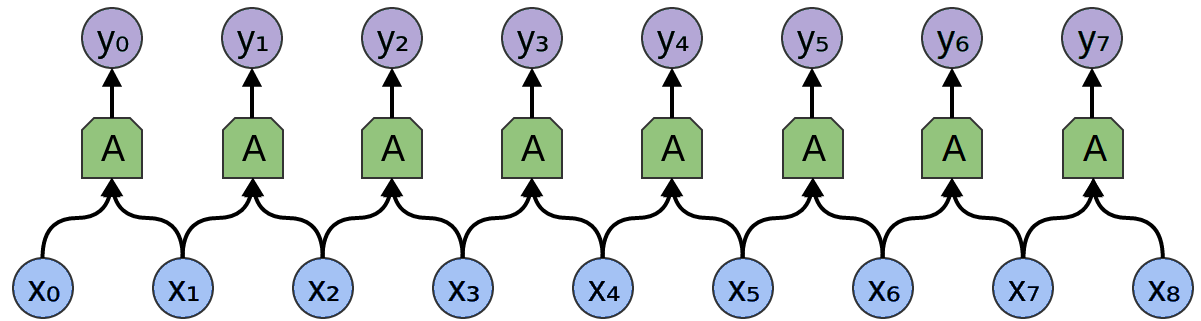
Convolution

1-dimensional convolution of a layer $A$ over an input sequence $x_1 ... x_8$ *

Convolution produces an output that is one rank higher than the convolved layer, e.g. convolving a layer that produces a scalar output would yield a vector.

Since each application of the convolved layer only sees a (typically small) window of the input, convolution is useful for detecting local features in the input. In an image processing task, these local features might be the edges of objects.

Useful for: Detecting local features in the input

Recurrence

The application of a layer to a sequence of inputs, where the result of processing one element of the sequence can influence the next.

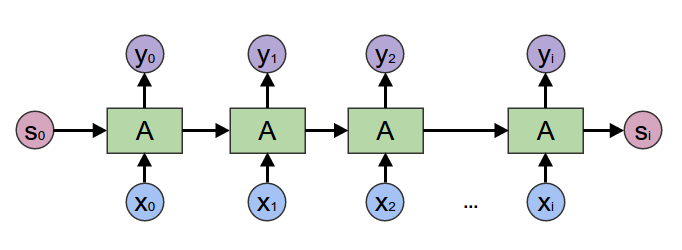
A recurrent nerual network

Recurrent application of a layer $A$ over an input sequence $x_1 ... x_i$ yeilding a sequence of outputs $y_1 ... y_i$ and a final hidden state $s_i$ *

Recurrence allows for the stateful processing of a sequence of inputs. What all recurrent neural networks have in common is:

They process sequences of inputs
The processing of one element of a sequence can influence the processing of the next

The way that the processing of one input influences the next depends on the layers used.

The simplest recurrent neural network uses a vanilla feedforward layer. In this architecture, the output vector from the application of the layer to one element of the input sequence is concatenated with the next vector in the input sequence.

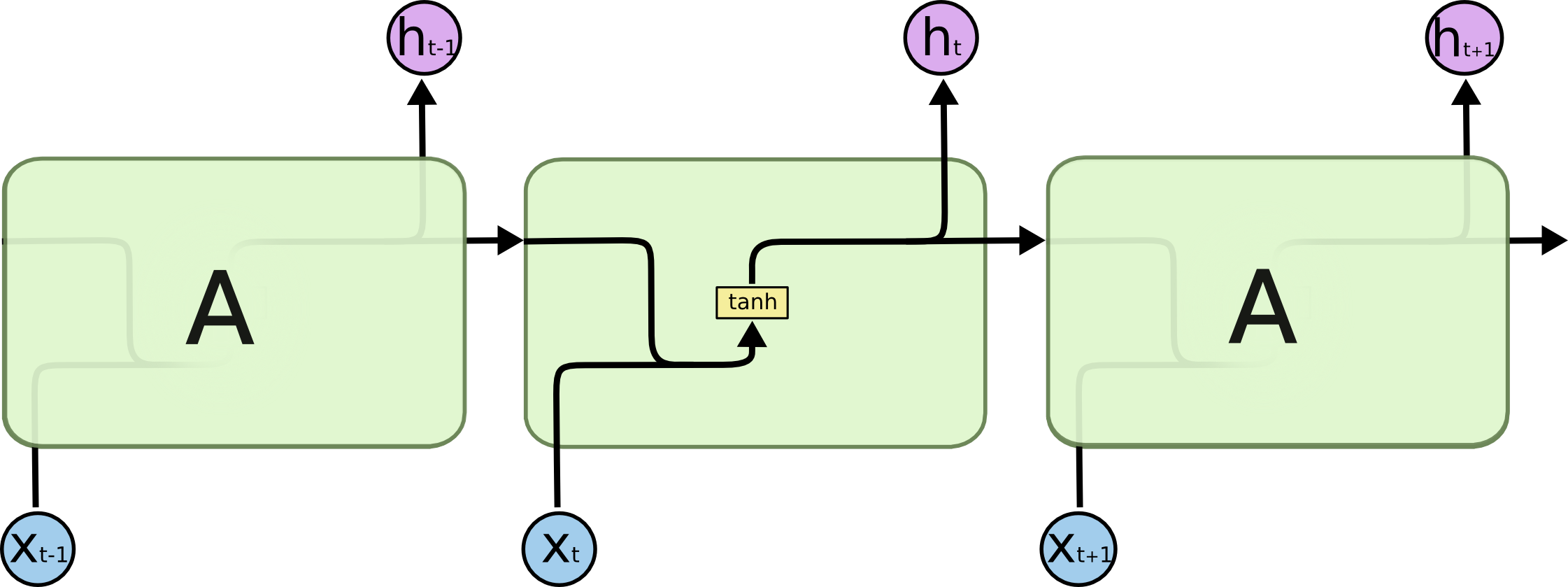
A simple recursive nerual network

The recurrent application of a vanilla layer with a $tanh$ nonlinearity to a sequence $x$ . At each time step $t$ , the previous hidden state $h_{t-1}$ is concatenated with the current element of the input sequence $x_t$ , which is then passed through the vanilla layer to generate the new hidden state $h_t$ .*

In this way, previous hidden state of the network can influence the network’s new hidden state, allowing the network to gradually build up state as it processes the sequence.

Useful for: Stateful sequence processing

Recursion

The recursive application of a layer to a tree-structured input.

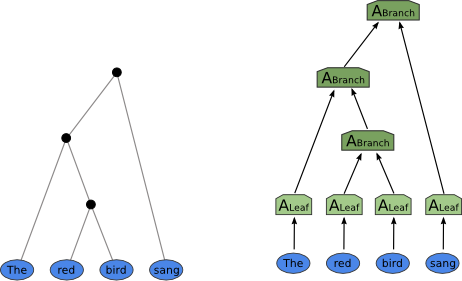
A recursive nerual network

In this architecture, the vectors for each word are first processed by a vanilla layer $A_{Leaf}$ before being combined through the recursive application of a layer $A_{Branch}$ according to the parse structure shown on the left.*

The input to a recursive neural network is a tree of vectors. Starting at the bottom of the tree, we apply a layer to each internal node. This layer takes the vectors for the children of that node and produces a vector that represents the entire subtree rooted at that node. We follow this procedure until we reach the root of the tree, yeilding a vector that represents the entire tree.

Useful for: Processing inputs with recursive structure, like sentence parse trees.

Acknowledgements

Many thanks to Chris Olah, whose blog and especially the post Neural Networks, Types, and Functional Programming inspired this project. Chris was also kind enough to allow me to use some of the excellent figures he made for that post and his post on Understanding LSTM Networks.